gaussLaplacianScheme(1/3): Theory and implementation in OpenFOAM

How the discretisation of the laplacian term is done? explicit evaluations, orthogonal corrections …

Notes made while reading through report by Jesper Roland¹. This report has detailed explanation on laplacianScheme abstract class, various macros like TypeName, New,… etc.

Options for laplacian scheme

A typical system/fvSchemes will read like below:

laplacianSchemes
{
laplacian(gamma,phi) Gauss linear corrected;
}

Gauss is the only laplacian scheme
linear is the keyword that tells how to interpolate the diffusion coefficient gamma from cell centres to cell faces.
corrected is the keyword that tells how to treat the non-orthogonal term. Valid schemes are : 7(corrected faceCorrected limited linearFit orthogonal quadraticFit uncorrected)

Generally the uncorrected and orthogonal schemes are only recommended for meshes with very low non-orthogonality (e.g. maximum 5 deg). The corrected scheme is generally recommended, but for maximum non-orthogonality above 70 deg, limited may be required. At non-orthogonality above 80 deg, convergence is generally hard to achieve.².

The gaussLaplacianScheme is dfined as gaussLaplacianSchem<Type, GType> where, Type is the type of $\phi$ which are scalar, vector, sphericalTensor, symmTensor and tensor. GType is the type of diffusion coefficient gamma which are also could be of the above types.

The flow of calls

Step 1: What solver calls

The call fvm::laplacian(DT, T) in line no 93 of the solvers/basic/laplacianFoam/laplacianFoam.C (code below) calls fvm::laplacian(gamma, phi) which is defined in src/finiteVolume/finiteVolume/fvm/fvmLaplacian.C line number 307.

laplacianFoam.C :
fvScalarMatrix TEqn
(
  fvm::ddt(T) - fvm::laplacian(DT, T)
  ==
  fvOptions(T)
); 

fvmLaplacian.C  :

template<class Type, class GType>
 tmp<fvMatrix<Type>>
 laplacian
 (
     const GeometricField<GType, fvsPatchField, surfaceMesh>& gamma,
     const GeometricField<Type, fvPatchField, volMesh>& vf
 )
 {
     return fvm::laplacian
     (
         gamma,
         vf,
         "laplacian(" + gamma.name() + ',' + vf.name() + ')'
     );
 }

Step 2: fvm::laplacian to fv::laplacianScheme

There are 16 different member functions in this fvmLaplacian.C file. A call to any of the laplacian function end up calling fvm::laplacian(gamma, phi, name) shown below:

 template<class Type, class GType>
 tmp<fvMatrix<Type>>
 laplacian
 (
     const GeometricField<GType, fvPatchField, volMesh>& gamma,
     const GeometricField<Type, fvPatchField, volMesh>& vf,
     const word& name
 )
 {
     return fv::laplacianScheme<Type, GType>::New
     (
         vf.mesh(),
         vf.mesh().laplacianScheme(name)
     ).ref().fvmLaplacian(gamma, vf);
 }

if the diffusivity γ is a volume field, i.e. the values are placed in the cell-centres. The function returns the output from the function laplacianScheme::fvmLaplacian in the class laplacianScheme. The call to laplacianScheme::fvmLaplacian is performed by first calling the selector function fv::laplacianScheme::New, which returns an output of type <tmp>. This output calls the function ref() from the class tmp. The output of ref() is a reference to the new object of type laplacianScheme. From this new object we call the function laplacianScheme::fvmLaplacian with input gamma and vf.

 laplacianScheme.C #88:

template<class Type, class GType>
 tmp<fvMatrix<Type>>
 laplacianScheme<Type, GType>::fvmLaplacian
 (
     const GeometricField<GType, fvPatchField, volMesh>& gamma,
     const GeometricField<Type, fvPatchField, volMesh>& vf
 )
 {
     return fvmLaplacian(tinterpGammaScheme_().interpolate(gamma)(), vf);
 }

The function laplacianScheme::fvmLaplacian returns fvmLaplacian(tinterpGammaScheme_().interpolate(gamma)(), vf)
which is a call to the function fvmLaplacian in the class, that is associated with the type name, which has been specified in the system/fvSchemes under laplacianSchemes, since this input is being passed to the New function in laplacianScheme. If we write the keyword Gauss in laplacianSchemes, then fvmLaplacian(tinterpGammaScheme_().interpolate(gamma)(), vf) is a call to the function gaussLaplacianScheme::fvmLaplacian in the class gaussLaplacianScheme.

Gauss theorem

Evaluation of the lalpacian term make use of Gauss theorem.

\begin{equation} \int_{V} \nabla . (\gamma \nabla\phi) dV \small{=} \intop_{S} ds. (\gamma \nabla\phi) \small{=} \sum_{f} S_{f}.(\gamma \nabla\phi)_{f} \end{equation}

For scalar diffusion coefficient

(1) becomes,

\begin{equation} \sum_{f} S_{f}.(\gamma \nabla\phi)_{f} =\sum_{f} \gamma_{f} |S_{f}|n_{f.}(\nabla \phi)_{f} \end{equation}

where , $n_{f}$ is the unit area vector obtained as $n_{f} = \frac{S_{f}}{|S_{f}|}$ .

For an orthogonal mesh, $(\nabla \phi)_{f}$ can be calculated exactly from the cell values across the face as the fraction of difference in cell centre value to distance between the cell centres. Hence (1) for orthogonal mesh become:

\begin{equation} \int_{V_{P}} \nabla . (\gamma \nabla\phi) dV = \sum_{f} \gamma_{f} |S_{f}|n_{f.} \frac{\phi_{N}-\phi_{P}}{|d|} \end{equation}

Implementation for scalar diffusion coefficient

The discretization of the laplacian term can be separated into an uncorrected and a corrected discretization. The uncorrected part includes the implicit discretization (orthogonal mesh and implicit part for non-orthogonal mesh) and contributions from boundary conditions. The corrected part of the discretization includes the explicit discretization, which is used to correct the implicit discretization, for example due to mesh non orthogonolity.

The scalar specialisation of gaussLaplacianScheme is implemented in gaussLaplacianSchemes.C

Foam::fv::gaussLaplacianScheme<Foam::Type, Foam::scalar>::fvmLaplacian         \
(                                                                              \
    const GeometricField<scalar, fvsPatchField, surfaceMesh>& gamma,           \
    const GeometricField<Type, fvPatchField, volMesh>& vf                      \
)                                                                              \
{                                                                              \
    const fvMesh& mesh = this->mesh();                                         \
                                                                               \
    GeometricField<scalar, fvsPatchField, surfaceMesh> gammaMagSf              \
    (                                                                          \
        gamma*mesh.magSf()                                                     \
    );                                                                         \
                                                                               \
    tmp<fvMatrix<Type>> tfvm = fvmLaplacianUncorrected //explained just below \
    (                                                                          \
        gammaMagSf,                                                            \
        this->tsnGradScheme_().deltaCoeffs(vf),                                \
        vf                                                                     \
    );                                                                         \
    fvMatrix<Type>& fvm = tfvm.ref();  

//check if non-orthogonal correction specified ....continued after explaining correction \

fvmLaplacianUncorrected:

template<class Type, class GType>
tmp<fvMatrix<Type>>
gaussLaplacianScheme<Type, GType>::fvmLaplacianUncorrected
(
    const surfaceScalarField& gammaMagSf,
    const surfaceScalarField& deltaCoeffs,
    const GeometricField<Type, fvPatchField, volMesh>& vf
)
{
    tmp<fvMatrix<Type>> tfvm
    (
        new fvMatrix<Type>
        (
            vf,
            deltaCoeffs.dimensions()*gammaMagSf.dimensions()*vf.dimensions()
        )
    );
    fvMatrix<Type>& fvm = tfvm.ref();

    fvm.upper() = deltaCoeffs.primitiveField()*gammaMagSf.primitiveField();
    fvm.negSumDiag();

    ..............Add boundary contribution..............

    return tfvm;
}

The function is static, so it applies to all objects, when it is called from the class. The function needs gammaMagSf = $\gamma_{f} |S_{f}|$ , deltaCoeffs = $n_{f} = \frac {n_{f}}{|d|}$ ( = $\frac{1}{|d|}$ for orthogonal mesh as $|n_{f}|$ =1) and the dependent variable $\phi$ , which is a volume field.

In fvmLaplacianUncorrected, first an fvMatrix object(tfvm) is defined. Then its upper triangle is filled by

fvm.upper() = deltaCoeffs.primitiveField()*gammaMagSf.primitiveField(); //((1/|d|)*gamma_f*Sf)

in case of orthogonal correction, deltaCoeffs are modified to (replaced by) nonOrthDeltaCoeffs ( $\frac{1}{n_{f}.d}$ ) . This will be explained in the code description of non-orthogonal correction.

Then diagonal coefficients are evaluated by invoking fvm.negSumDiag() as

a_{C} = -(a_{E}+a_{W}+a_{S}+a_{N})

The above equation is implemented by looping over all the faces and making use of lowerAddr() and upperAddr() which carried the info about owner and neighbour of the face respectively. lower() and upper() provide the coefficients. Hence, fvm.negSumDiag() reads:

void Foam::lduMatrix::negSumDiag()
{
const scalarField& Lower = const_cast<const lduMatrix&>(*this).lower();
const scalarField& Upper = const_cast<const lduMatrix&>(*this).upper();
scalarField& Diag = diag();
}
const labelUList& l = lduAddr().lowerAddr();
const labelUList& u = lduAddr().upperAddr();
for (register label face=0; face<l.size(); face++)
{
Diag[l[face]] -= Lower[face];
Diag[u[face]] -= Upper[face];
}

boundary contribution will be explained later.

Non-orthogonal mesh

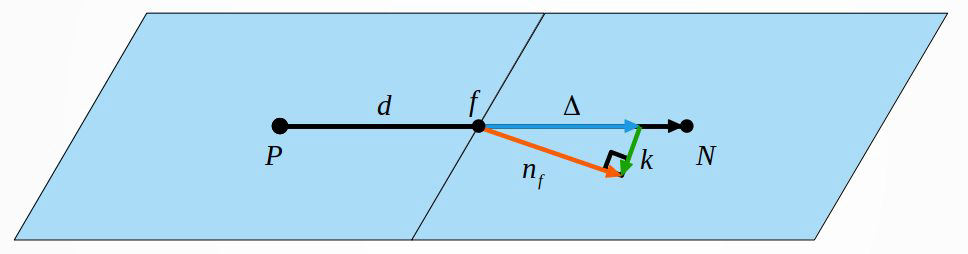
Over relaxed version of component splitting. Image source ³

In non orthogonal mesh case, the surface normal vector $n_{f}$ is split to along $d$ ( $\Delta$ ) and perpendicular to $n_{f}$ ( $k$ ). Hence (3) becomes

\begin{equation} n_{f.} \frac{\phi_{N}-\phi_{P}}{|d|} = \underbrace{\Delta \frac{\phi_{N}-\phi_{P}}{|d|}}_{\text{orthogonal}} + \underbrace{k.(\nabla \phi)_{f}}_{\text{non orthogonal}} \end{equation}

\begin{equation} \Delta = \frac{d}{d.n_{f}}=\underbrace{d}_{\text{delta}} \underbrace{\frac{1}{d.n_{f}}}_{\text{nonOrthDeltaCoeffs}} \end{equation}

To avoid possible division by zero,

\begin{equation} \Delta = \frac{d}{d.n_{f}}=\underbrace{d}_{\text{delta}} \underbrace{\frac{1}{max(d.n_{f}, 0.5|d|)}}_{\text{nonOrthDeltaCoeffs}} \end{equation}

\begin{equation} k = n_{f} - d \frac{1}{max(d.n_{f}, 0.5|d|)} \end{equation}

Explicit evaluation of gradient term $(\nabla \phi)_{f}$ in non orthogonal part (4) is computed in following way. Step 1:

\begin{CD} \phi_{P}, \phi_{N} @>f_{x}\phi_{P}+(1-f_{x})\phi_{N}>> \phi_{f}@>\frac{1}{V_{P}}\sum S_{f}\phi_{f}>> (\nabla \phi)_{P}, (\nabla \phi)_{N} \end{CD}

Where, $f_{x} = \frac{fN}{d}$ . Cell centred value is interpolated to get face value. Gauss theorem is applied to get cell centered gradient value.

In step 2:

\begin{CD} (\nabla \phi)_{P}, (\nabla \phi)_{N} @>f_{x}(\nabla\phi)_{P}+(1-f_{x})(\nabla\phi)_{N}>> (\nabla \phi)_{f} \end{CD}

Again interpolation is carried out to get the face value of the gradient. Now, eqn (4) can be calculated.

The calculation of deltaCoeffs() is carried out by surface normal gradient schemes.

Surface normal gradient schemes

snGradScheme abstract base class

The class snGradScheme is the abstract base class for surface normal gradient schemes, and the function deltaCoeffs(vf) is defined as pure virtual function in the snGradScheme class declaration. snGradScheme.H is located src/finiteVolume/finiteVolume/snGradSchemes/snGradScheme/snGradScheme.H.

//- Return the interpolation weighting factors for the given field
virtual tmp<surfaceScalarField> deltaCoeffs
(
            const GeometricField<Type, fvPatchField, volMesh>&
) const = 0;

However, we have selected corrected keyword for the non-orthogonal term.

correctedSnGrad Scheme

Member functions

deltaCoeffs() : returning nonOrthDeltaCoeffs
virtual bool corrected() :Return true if this scheme uses an explicit correction (yet to decifer)
fullGradCorrection(): just returns the inner product of the interpolated gradient at the face with the nonOrthCorrectionVector
correction(): Just return the value of fullGradCorrection()

correctedSnGrad.H shows

        //- Return the interpolation weighting factors for the given field
        virtual tmp<surfaceScalarField> deltaCoeffs
        (
            const GeometricField<Type, fvPatchField, volMesh>&
        ) const
        {
            return this->mesh().nonOrthDeltaCoeffs();
        }

nonOrthDeltaCoeffs()

The function nonOrthDeltaCoeffs() is a virtual function of class surfaceInterpolation. It is defined in basicFvGeometryScheme.C and is included in surfaceInterpolation.C. The fvMesh inherits from surfaceInterpolation class hence it can call nonOrthDeltaCoeffs()

    surfaceScalarField& nonOrthDeltaCoeffs = tnonOrthDeltaCoeffs.ref();
    nonOrthDeltaCoeffs.setOriented();

    // Set local references to mesh data
    const volVectorField& C = mesh_.C();
    const labelUList& owner = mesh_.owner();
    const labelUList& neighbour = mesh_.neighbour();
    const surfaceVectorField& Sf = mesh_.Sf();
    const surfaceScalarField& magSf = mesh_.magSf();
    forAll(owner, facei)
    {
        vector delta = C[neighbour[facei]] - C[owner[facei]];//d
        vector unitArea = Sf[facei]/magSf[facei];//nf
        // Standard cell-centre distance form
        //NonOrthDeltaCoeffs[facei] = (unitArea & delta)/magSqr(delta);//nf.d/(d.d)

        // Slightly under-relaxed form
        //NonOrthDeltaCoeffs[facei] = 1.0/mag(delta);//1/|d|

        // More under-relaxed form
        //NonOrthDeltaCoeffs[facei] = 1.0/(mag(unitArea & delta) + VSMALL);//1/(nf.d+eps)

        // Stabilised form for bad meshes
        nonOrthDeltaCoeffs[facei] = 1.0/max(unitArea & delta, 0.05*mag(delta));// 1/max(nf.d, 0.05d)
    }
//for boundary
    surfaceScalarField::Boundary& nonOrthDeltaCoeffsBf =
        nonOrthDeltaCoeffs.boundaryFieldRef();

    forAll(nonOrthDeltaCoeffsBf, patchi)
    {
        fvsPatchScalarField& patchDeltaCoeffs = nonOrthDeltaCoeffsBf[patchi];

        const fvPatch& p = patchDeltaCoeffs.patch();

        const vectorField patchDeltas(mesh_.boundary()[patchi].delta());

        forAll(p, patchFacei)
        {
            vector unitArea =
                Sf.boundaryField()[patchi][patchFacei]
               /magSf.boundaryField()[patchi][patchFacei];

            const vector& delta = patchDeltas[patchFacei];

            patchDeltaCoeffs[patchFacei] =
                1.0/max(unitArea & delta, 0.05*mag(delta));
        }

        // Optionally correct
        p.makeNonOrthoDeltaCoeffs(patchDeltaCoeffs);
    }
    return tnonOrthDeltaCoeffs;
}

Correction vector k and faceFluxCorrectionPtr()

k vector (corrVecs) is calculated in basicFvGeometryScheme.C as follows:

    forAll(owner, facei)
    {
        vector unitArea = Sf[facei]/magSf[facei];
        vector delta = C[neighbour[facei]] - C[owner[facei]];

        corrVecs[facei] = unitArea - delta*NonOrthDeltaCoeffs[facei];
    }

This is exactly (7).

   //check if non-orthogonal corrn specified ....continuing                                                                           
                                                                               \
    if (this->tsnGradScheme_().corrected())                                   \
    {                                                                          \
        if (mesh.fluxRequired(vf.name()))                                      \
        {                                                                      \
            fvm.faceFluxCorrectionPtr() = new                                  \
            GeometricField<Type, fvsPatchField, surfaceMesh>                   \
            (                                                                  \
                gammaMagSf*this->tsnGradScheme_().correction(vf)               \
            );                                                                 \
                                                                               \
            fvm.source() -=                                                    \
                mesh.V()*                                                      \
                fvc::div                                                       \
                (                                                              \
                    *fvm.faceFluxCorrectionPtr()                               \
                )().primitiveField();                                          \
        }                                                                      \
        else                                                                   \
        {                                                                      \
            fvm.source() -=                                                    \
                mesh.V()*                                                      \
                fvc::div                                                       \
                (                                                              \
                    gammaMagSf*this->tsnGradScheme_().correction(vf)           \
                )().primitiveField();                                          \
        }                                                                      \
    }                                                                          \
                                                                               \
    return tfvm;                                                               \
}                                                                         \

this->tsnGradScheme_().correction(vf) is $k. (\nabla \phi)_{f}$ in (4).

fullGradCorrection and correction are defined in src/finiteVolume/finiteVolume/snGradSchemes/correctedSnGrad/correctedSnGrad.C.

correction just returns the values of fullGradCorrection(vf). fullGradCorrection just returns the inner product of the interpolated gradient at the face with the nonOrthCorrectionVector

template<class Type>
Foam::tmp<Foam::GeometricField<Type, Foam::fvsPatchField, Foam::surfaceMesh>>
Foam::fv::correctedSnGrad<Type>::fullGradCorrection
(
    const GeometricField<Type, fvPatchField, volMesh>& vf
) const
{
    const fvMesh& mesh = this->mesh();

    // construct GeometricField<Type, fvsPatchField, surfaceMesh>
    tmp<GeometricField<Type, fvsPatchField, surfaceMesh>> tssf =
        linear<typename outerProduct<vector, Type>::type>(mesh).dotInterpolate
        (
            mesh.nonOrthCorrectionVectors(),
            gradScheme<Type>::New
            (
                mesh,
                mesh.gradScheme("grad(" + vf.name() + ')')
            )().grad(vf, "grad(" + vf.name() + ')')
        );
    tssf.ref().rename("snGradCorr(" + vf.name() + ')');

    return tssf;
}


template<class Type>
Foam::tmp<Foam::GeometricField<Type, Foam::fvsPatchField, Foam::surfaceMesh>>
Foam::fv::correctedSnGrad<Type>::correction
(
    const GeometricField<Type, fvPatchField, volMesh>& vf
) const
{
    const fvMesh& mesh = this->mesh();

    // construct GeometricField<Type, fvsPatchField, surfaceMesh>
    tmp<GeometricField<Type, fvsPatchField, surfaceMesh>> tssf
    (
        new GeometricField<Type, fvsPatchField, surfaceMesh>
        (
            IOobject
            (
                "snGradCorr("+vf.name()+')',
                vf.instance(),
                mesh,
                IOobject::NO_READ,
                IOobject::NO_WRITE
            ),
            mesh,
            vf.dimensions()*mesh.nonOrthDeltaCoeffs().dimensions()
        )
    );
    GeometricField<Type, fvsPatchField, surfaceMesh>& ssf = tssf.ref();
    ssf.setOriented();

    for (direction cmpt = 0; cmpt < pTraits<Type>::nComponents; cmpt++)
    {
        ssf.replace
        (
            cmpt,
            correctedSnGrad<typename pTraits<Type>::cmptType>(mesh)
           .fullGradCorrection(vf.component(cmpt))
        );
    }

    return tssf;
}

fvc::snGrad(field,name) defined in /finiteVolume/finiteVolume/fvc/fvcSnGrad.C return a temperory object of snGradeScheme as per the keyword entered in system/fvSchemes. The selector function fv::snGradScheme<Type>::New is called here.

Disabguation with snGrad() in fvPatchField class

snGrade() in fvPatchField class return patch-normal gradient.Each boundary patch may implement its own method to calculate the boundary snGrad. Some boundary patch does not implements its version hence the default snGrad() take over.

 template<class Type>
 Foam::tmp<Foam::Field<Type>> Foam::fvPatchField<Type>::snGrad() const
 {
     return patch_.deltaCoeffs()*(*this - patchInternalField());
 }

As we can see above, it does not take care of non orthogonal correction. However, an orthogonal corrected version is available in fixedDisplacementFvPatchVectorField.C as:

vectorField n = this->patch().nf();
 vectorField delta = this->patch().delta();
 //- correction vector T
 vectorField k = delta - n*(n&delta);

 return 
 (
   *this 
  - (patchInternalField() + (k&gradField.patchInternalField()))
  )*this->patch().deltaCoeffs();

Phillip Cardiff here

Miscellaneous

pTraits

pTraits is merely a wrapper class, which unifies access to certain properties for all primitive types ⁴ ⁵

dotInterpolate

This interpolates the field and “dots” the resulting face-values with the vector field provided which removes the need to create a temporary field for the interpolate. This reduces the peak storage of OpenFOAM caused by the divergence of the gradient of vector fields, improves memory management and under some conditions decreases run-time. ⁶. Hence, dotInterpolate interpolate the element value of $\Delta \phi$ to faces and dot with k vector.

FluxRequired option in fvSchemes

In laplacian, the flux at each cell face is calculated as gammaMagSf*this->tsnGradScheme_().correction(vf). If this flux information is useful after the solution of the equation, then we need to add it to the fluxrequired list in fvSchemes.

faceFluxCorrectionPtr() returns the pointer faceFluxCorrectionPtr_. Hence faceFluxCorrectionPtr_ is assigned with a value gammaMagSf*this->tsnGradScheme_().correction(vf)

The face flux correction pointer faceFluxCorrectionPtr is used when we are calling the flux() method in the fvMatrix class. The flux() method returns the flux calculated from the matrix coefficients, and therefore we have to add the explicit contribution to get the correct flux, when we want to account for mesh non orthogonality. The flux() method is implemented in fvMatrix.C at Line 923-1009, and faceFluxCorrectionPtr is used at Line 1005, where it is added to the flux computed from the matrix coefficients

fvMatrx.C:

    if (faceFluxCorrectionPtr_)
    {
        fieldFlux += *faceFluxCorrectionPtr_;
    }

flux()

Calculation of flux (demonstrating use of faceFluxCorrectionPtr) ⁷

setOriented()

setOriented()⁸

Bruno’s explanation on gaussLaplacianScheme

gauss linear zeroth order

Non-orthogonal and skewed mesh

Skewness correction is mentioned at page 254 [3] in relation to the description of the diffusion term. The skewness correction of the gradient is discussed at page 275-280 [3] and a presentation of how to implement a gradient computed using Gauss’ theorem and interpolation that account for mesh skewness is presented at page 297 [3]. The face gradient in the non orthogonal term from the laplacian discretization can be corrected for mesh skewness using the following settings for a dependent variable φ

gradSchemes
{
default       none;
grad(phi)     Gauss skewCorrected linear;
}

The source files of this scheme is found in the folder
$FOAM_SRC/finiteVolume/interpolation/surfaceInterpolation/schemes/skewCorrected